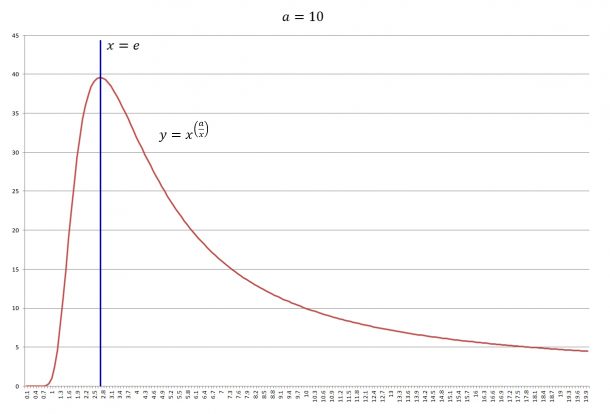
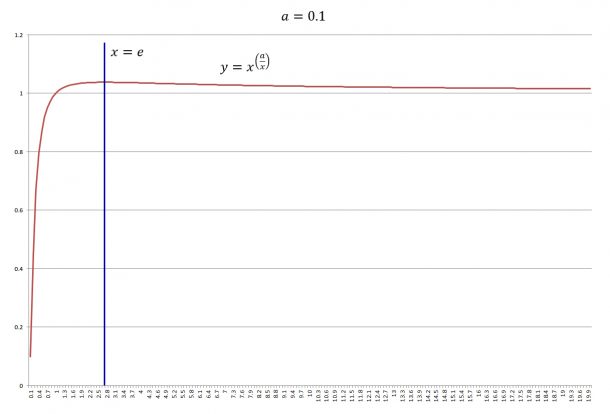
前々回の記事「試験的考察 被写界深度」で、被写界深度を決める要因として、
焦点距離、絞り値、被写体距離、許容錯乱円
をあげましたが、それらがどの程度効いてくるのか、簡単なシミュレーションをしてみました。
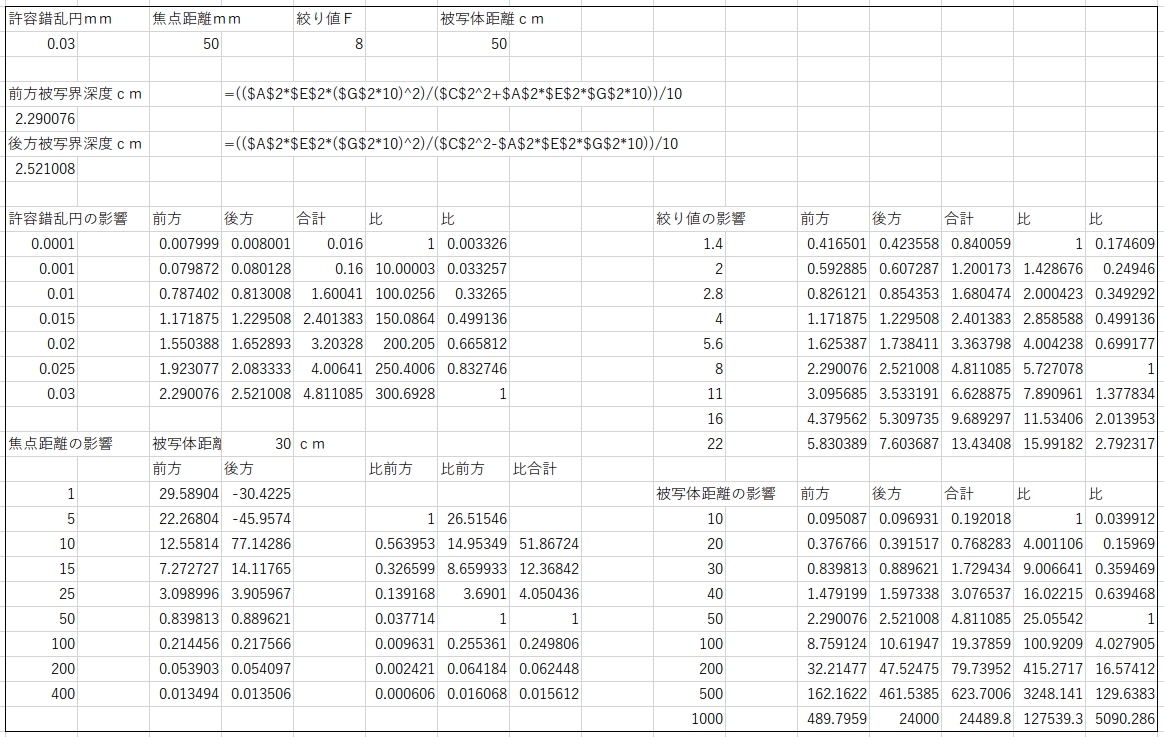
式は、ネット上で広く紹介されている近似式です。マクロ撮影では誤差が大きくなるとされています。
($A$2:許容錯乱円直径 $C$2:レンズの焦点距離 $E$2:絞り値 $G$2:被写体距離)
いずれも、ひとつの変数のみを変えています。実際の撮影現場では、同時にいくつも変数が変わる(撮像素子サイズが変われば許容錯乱円も焦点距離も被写体距離も絞り値も変わる可能性)ことも多いのですが、ひとつの目安としては有効な計算だと思います。
はじめに、フルサイズの標準的事例についてのテスト計算をしています。
中段以降で、それぞれの変数を変えた場合に被写界深度にどの程度影響があるかを計算しています。
焦点距離の影響の計算の場合のみ、極端に短い焦点距離に対応する(なるべくマイナスの数字が出ないようにするなど)ため、被写体距離を30cmにしています。そのため長焦点では非現実的な例となっていますが、計算のための便宜と見てください。
さて、この表から、非常に大雑把ではありますが、以下のことが言えると思います。
許容錯乱円は、ほぼリニアに影響する(半分になれば、深度もほぼ半分になる)。
絞り値も、ほぼリニアに影響する(半分になれば、深度もほぼ半分になる)。
そもそも、式においてこの二つはセットで出てくるのでウエイトは当然同じになります。
焦点距離は、ほぼ(逆)2乗で効いてくる(焦点距離が倍になれば、深度はほぼ1/4になる)。
被写体距離も、ほぼ2乗で効いてくる(距離が半分になれば、深度はほぼ1/4になる)。
ただいずれの場合も、深度が浅くなる側に、若干厳しくなります。
比較対象に大きな差がある場合には誤差が大きくなりますが、2倍程度の差であれば、おおむねこういえそうです。
ちなみに、私は古い人間ですので、フルサイズの許容錯乱円の計算では、フィルム時代の0.03mmを使用しています。
以上から、撮像素子の小さなカメラで、同じ場所から同じ画角でしかも同じ絞り値で撮影すれば、許容錯乱円より焦点距離の効果が勝り、深度は深くなることがわかります。
ただし絞り値が同じにならない場合、深度を深くする効果は弱くなります。
たとえば Canon S120 (センサーサイズ 1/1.7型)の場合、フルサイズに比べて4.6倍相当に変数が変わります。許容錯乱円で4.6倍損する代わりに、焦点距離で4.6^2倍得する形になります。しかし最小絞りがF8です。仮にフルサイズをF22とすれば2.75倍(F32とすれば4倍)の違いです。
このため、F22のフルサイズとの比較では、結局1.7倍ほどの効果にとどまります(あくまでざっくりとした計算です)。
なおここで、許容錯乱円は、画素ピッチレベルのシビアなものではなく、フィルムカメラ風に、フルサイズをたとえば0.03mmとして、センサーサイズに比例して小さくなる、という形の計算をしています。後で拡大することになるので、その分厳しくなる、という比例的計算です。
実際に、フルサイズ(許容錯乱円0.03mm)・焦点距離50mm・被写体距離50cm・F22 と、 1/1.7型(許容錯乱円0.0065mm)・焦点距離10.8mm・被写体距離50cm・F8 とを比較すると、
フルサイズ:前方被写界深度 5.83 後方被写界深度 7.60 合計 13.43
1/1.7型:前方被写界深度 9.11(1.56倍) 後方被写界深度 14.34(1.89倍) 合計 23.46 (1.75倍)
となりました。単位はcmです。
絞りの差で2倍を切ってしまいましたが、深度の合計値では、10cm以上の広さがあります。模型撮影などでは大きな差で、やはり、撮像素子サイズが小さいほど深度が深い、は一般論として正しいと感じました。
広角か望遠かについても、以下のようなことが考えられます。
画角と焦点距離は、ざっくり言って反比例関係にあり、また、被写体距離と被写体の見かけの大きさに反比例関係がある、と見れば、被写体の見かけの大きさを同じにする場合、焦点距離が半分なら、半分の距離で写すことになる、となるのではないでしょうか。
とすると、広角は望遠に比べ、焦点距離で約2乗分得するが、被写体距離で約2乗分損をする、ということになります。
具体的な数値は計算の必要がありますが、「大差ないのでは」という疑いが生じます(広角と望遠では比が2倍を大きく超えてきますので、単純な計算との誤差がそれなりに生じているであろうことには注意が必要です)。
例として、フルサイズ(許容錯乱円0.03mm)・F22において、焦点距離28mmと焦点距離200mmとを比較してみました。
200mmの画角は横が10.29度(Wikipediaより)なので半分が5.145度、被写体距離を200cmとして、横半分に200*tan(5.145°)=18.01cm入ることになります。28mmの横画角の半分は32.75度(同)なので、横半分が18.01cmになる距離は、18.01*(1/tan(32.75°))=28cm、ほぼ焦点距離と比例でした。
その場合の被写界深度は、
焦点距離28mm:前方被写界深度 5.34 後方被写界深度 8.63 合計 13.97
焦点距離200mm:前方被写界深度 6.39 後方被写界深度 6.83 合計 13.21
となって、28mmのほうがわずかに広いものの、大差なし、という結果となりました(単位cm)。
参考までに、同様の計算をすると、24mmの合計深度が14.32 35mmが13.72 50mmが13.44 100mmが13.28 500mmが13.24 などとなり、わずかに広角側が有利なものの、大きな差ではありません。
やや意外感のある結果です。
画面の横幅を同じにする、という前提に甘さがあるのかもしれません。「画面の中での被写体の長さの割合を同じにする」というのがより正しいのだと思いますが、具体的な数値の置き方はどうなるのか。被写体が斜めに置かれている場合はどうするか。
仮に広角の被写体距離が30cmなら、合計深度は16.19cmとなって、少し広角有利とはなります。
ちなみに、絞り値をF22に固定で、被写体距離を、単純に焦点距離の10倍(つまり50mmなら50cm)とした場合、焦点距離が500mmであっても28mmであっても、合計深度は13cm台です(広角になるにつれ少しずつ大きくなります)。
許容錯乱円を、最近の基準値0.026mmとすると、合計深度は11cm台と、少し厳しくなります。
少なくとも、広角のほうが圧倒的に有利であるとまではいえない、という印象です。
以上から、焦点距離の選択については、撮影意図(プロポーションの選択など)や撮影環境で決定してよいのではと思います。
撮影環境については、たとえば広角の場合、後ろが広く入りますので、(たとえ青空でも)背景も広く用意しなくてはなりません。望遠の場合、背景は小さくて済みます。また、広角で写せるほど近寄れない(あるいは逆に望遠が使えるほど引けない)、という場合も考えられます。
トリミングの有効性について
同じ焦点距離のレンズで、同じ絞り値で写す場合、少し距離をとって、少しトリミングする、という方法は、若干の画質低下と引き換えに、被写界深度を深くすることができます。被写体距離と許容錯乱円の効き方の差です。ざっくりした計算で、2乗分得をして、1乗分損をすることで、結果として1乗分得をする、というイメージです。
また、少し広角にして撮影し、少しトリミングする、という方法でも、同様の効果が期待できます。
ただ、あまり極端にトリミングすると、画素数の不足やレンズの収差の目立ちにより、画質の劣化が無視できなくなってきます。最終的に必要な画素数などを頭に入れながら撮影することも一つかと思います。
先の記事で作例にあげた写真は、ほぼ200mmの最短撮影距離で写しており、フルサイズをあまりトリミングしていないのですが、トリミング前提でもう少し引いて写せば、コンテナすべてにピントが合ったかもしれません。
以上、計算や考え方に誤りがあるかもしれませんが、意外感のある結果もありましたので、ご参考までに。