例:
10 を、足して 10 となるいくつかの数(すべて正の数とします)に分けます。
4+6 とか 2+3+5 とか 2+2+2+2+2 とか。
今度は、それらの数をかけます。つまり足し算の記号を掛け算にします。
4*6=24 2*3*5=30 2*2*2*2*2=32 などとなり、積の値は分割の仕方に応じてさまざまになります。
問:積が最も大きくなる分割方法を求む(最適分割問題)
分割の個数が同じならば、等分割にするのが最も積が大きくなります。4*6<5*5
ここから一般化して、数 a(ただし a>0)を p 個に等分割し、分割した数 x=(a/p) を p 乗して積を作る問題とします。
たとえば、a=10 の場合、
p=1 のとき、積 y=10
p=2 のとき、y=5*5=25
p=3 のとき、y=(10/3)^3=37.037037…
p=4 のとき、y=2.5^4=39.0625
p=5 のとき、y=2^5=32
p=10 のとき、y=1^10=1
となります。
さらに、y=x^p=(a/p)^p は pが整数でなくとも成立するので、整数個ではない分割をも認めることとします(ただし a>0, p>0)。つまり3.5個に分割して3.5乗する、という形も解として可能とします。
ここで、分割した数 x のほうから、a に x が何個あるか、という形で考えると、p=a/x なので、
y=x^(a/x) となり、等分割された数 x を定めれば、積 y が決まります。
x,y は正なので、対数をとって、log(y)=(a/x)log(x) として、両辺をxで微分すると、
(1/y)(dy/dx)=(a/x)(1/x)-(a/x^2)log(x)=(a/x^2)(1-log(x)) よって、
dy/dx=(x^(a/x))(a/x^2)(1-log(x))=a(x^((a/x)-2))(1-log(x))
ここで、x>0 のとき、x^((a/x)-2)>0 なので、極値は log(x)=1 つまり
x=e (=2.71828…) のときとなります。
また、導関数の正負は、1-log(x) の正負によりますから、0<x<e で導関数は正、e<x で導関数は負となります。
x<1 となると、y は(a が大きいときは急速に)0 に近づく一方、(厳密な証明は省きますが)x が非常に大きくなると、0乗に近くなり、y は 1 に近づきます。
したがって、x=e のときの極値は、極大値かつ最大値となります。
つまり、自然対数の底 e を単位として a を分割し、 e が何個あるか、という形にして、
e^(a/e) により積を求めれば、これが、a を分割して得られる最大の積となります。
これは、はじめに与えた数 a の如何に関わりません。
はじめの例において、a=10 の場合には、最大値は、x=e のとき、39.5986… となります。
(3.67879… 個に分割)
改めて見ると、4分割の場合の値 2.5^4=39.0625 は、かなりよい値といえますが、
2.5 が e=2.71828… に近い値であったためであったことがわかります。
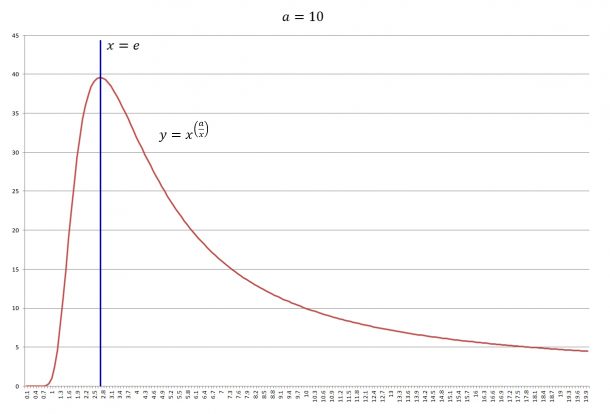
グラフにしてみると、x の変化に対する y の挙動がよくわかります。
以下は、y=x^(a/x) の、a=10 の場合のグラフです。
(Excelで計算およびグラフ作成:横軸が x, 縦軸が y)
x が 1 より小さくなると、0 に近い数を何回も掛け算することになるので、0 付近に張り付くようになります。x が大きくなると、0乗 (=1) に近づいていきますが、下がり方は比較的にゆっくりです。
最大値は、x=e のときです。なかなかきれいなグラフだと思います。
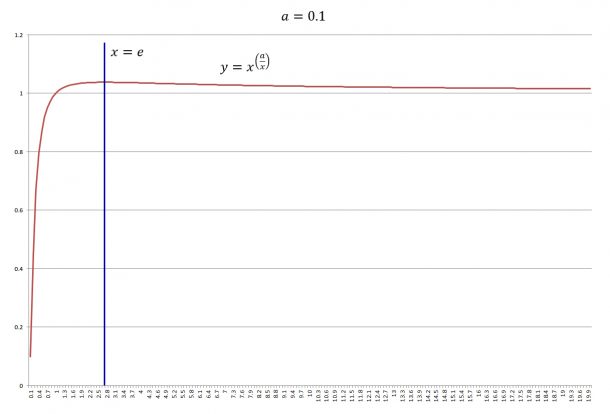
また、y が x=e のときに最大値をとることは、a が 1 より小さい数であっても当てはまります。
以下は、a=0.1 の場合のグラフです。
面白いのは、元の数 a が小さくても、y は、x>1 で、1 より大きくなることです。
x=1 のときに、必ず 1 を通ります(1^p の形なので)。また、x → ∞ での y の極限は 1 なので、
x>1 で、常に y>1 になります(0.01乗とかであっても、0乗(=1)よりは大きい)。
やはり、最大値は、x=e のときです。
なお、a=1 の場合は、グラフの形は、上掲2図の中間的なものになります。
自然対数の底 e (ネイピア数)は、円周率 π とは異なり、その特別さに関して、具体的イメージのわきにくい数だと思いますが、こういった、単純な掛け算の問題の最適解という形で、いわば掛け算で最も効率的に大きくなる数として現れます。
e の持つ特別な性質として、なかなか面白い例なのではと思います。
<追記>
(1) e^π と π^e の、どちらが大きいか、という問題があります。
上述の考察は、a^b(a,b>0:ただし底と指数の積 a*b は一定)の形の数において、a^b が最大であるのは、底を e にした場合(つまり e^(a*b/e) )である、ということができます。
今の問題では、底と指数の積は e*π で一定ですので、指数の形(a^b)の数は、e を底とした場合に最大になりますから、そこから直ちに、e^π > π^e であることがわかります。
(2) また、5^7 と 7^5 の比較(これは35をどう分割するかという問題)、あるいは、71^73 と 73^71 のような、ともに e より大きな数の底と指数の交換の場合、底が e に近い 5^7 , 71^73 のほうが大きいことが、上述の考察およびグラフから明らかです。
さらに、交換でなくとも、底と指数の積が一定であり、ともに底が e より大きい(あるいは小さい)数同士の比較においても、たとえば、3^8>4^6 のように、底の e への近さによって大小がわかります。
(3) x^y=y^x を満たす自然数(ただし x<y)、については、上述の考察およびグラフから明らかなように、交換して同じになる可能性は、一方が 1<x<e の場合のみです。つまり可能性のあるのは x=2 のみです。
もう一方の数については、3 は e に近すぎて 2^3<3^2、4 は 2^4=4^2=16 となって成立、5 は e から遠すぎて 2^5>5^2、二次関数 x^2 と指数関数 2^x の形から、それ以降はすべて x^2 のほうが小さい、となります(厳密に示すには、もう一度微分が必要かもしれません)。
この問題の場合、ペアがひとつしかないことを厳密かつ簡潔に示すには、f=log(x)/x から考察するのが筋のようです(x^y=y^x から、対数をとって整理して、log(x)/x=log(y)/y を導き、f=log(x)/x を微分してグラフを書くなど)。